UNIVERSIDAD AUTÓNOMA DE GUERRERO
PROGRAMA EDUCATIVO:
INGENIERO CIVIL
MÉTODOS NUMÉRICOS
ALUMNO: DANIEL GUADALUPE SALAS FLORES
DOCENTE: LORENA ALONSO GUZMAN
401 T.M.
- INTRODUCCIÓN
- SISTEMAS DE ECUACIONES LINEALES
- MATRICES
- MÉTODO DE GAUSS
- ELIMINACIÓN DE GAUSS
- REGLA DE CRAMMER
- MÉTODO DE GAUSS SEIDEL
- BIBLIOGRAFIA
INTRODUCCION
En este blog desarrolle el tema: sistemas de ecuaciones lineales. los procesos que estos llevan para darle solución a las funciones dadas.
SISTEMA DE ECUACIONES LINEALES
Un sistema de ecuaciones lineales es un conjunto de ecuaciones lineales que tienen mas de una incógnita. Las incógnitas aparecen en varias de las ecuaciones, pero no necesariamente en todas. Lo que hacen estas ecuaciones es relacionar las incógnitas entre si.
Por ejemplo:
3x + 2y = 1
x - 5y = 6
Se trata de un sistema de dos ecuaciones con dos incógnitas (x, y).
Resolver un sistema de ecuaciones consiste en encontrar el valor de cada incógnita para que se cumplan todas las ecuaciones del sistema.
La solución al sistema anterior es:
x = 1
y = -1
Pero no siempre existe solución, o bien pueden existir infinitas soluciones. Si hay una única solución (un valor para cada incógnita, como en el ejemplo anterior) se dice que el sistema es compatible determinado.
Para resolver sistemas ( lineales) de dos ecuaciones con dos incógnitas mediante los métodos que describiremos a continuación, que se basan en la obtención de una ecuación de primer grado.
- Sustitución: consiste en despejar o aislar una de las incógnitas (por ejemplo,x) y sustituir su expresión en la otra ecuación. De este modo, obtendremos una ecuación de primer grado con otra incógnita, y. Una vez resuelta, obtenemos el valor de x sustituyendo el valor de y que ya conocemos.
- Reducccion: consiste en operar con las ecuaciones como, por ejemplo, sumar o restar ambas ecuaciones, de modo que una de las incógnitas desaparezca. Así obtenemos una ecuación con una sola incógnita.
- Igualación: consiste en aislar en ambas ecuaciones la misma incógnita para poder igualar las expresiones, obteniendo así una sola ecuación.
SOLUCIÓN POR SUSTITUCIÓN
Despejamos en la primera ecuación la x:
x + y = 3 → x = 3 - y
Y la sustituimos en la segunda:
2x - y = 0 →
2 (3 - y) - y = 0 →
6 - 2y - y = 0 →
6 - 3y = 0 →
6 = 3y →
y = 6/3→
y = 2
Calculamos x sabiendo y:
x = 3 - y = 3 - 2 = 1
Por tanto la solución del sistema es:
x = 1, y = 2
SOLUCIÓN POR IGUALACIÓN
despejamos en ambas ecuaciones la y:
x + y = 3 → y = 3 - x
4x - y = 0 → y = 4x
como y = y, igualamos las expresiones y resolvemos la ecuación:
3 - x = 4x
3 = 5x
x = 3/5
Ahora, sustituimos el valor de la incógnita x = 3/5 en la primera de las ecuaciones anteriores para obtener y:
y = 3 - 3/5 = 12/5
Por lo tanto, la solución del sistema es:
x = 3/5, y= 12/5
SOLUCIÓN POR REDUCCION
Para sumar las ecuaciones y que desaparezcan una de las dos incógnitas, los coeficientes de dicha incógnita deben ser iguales pero de signo contrario. Para ello, multiplicamos por - 2 la primera ecuación.
x + y = 3
2x - y = 0
↓
-2x - 2y = -6
2x - y = 0
-----------
0x - 3y = -6
↓
-3y = -6
↓
y = -6/-3 = 2
Finalmente, sustituimos el valor de y = 2 en la primera ecuacion y la resolvemos:
x + y = 3 →
x + 2 = 3 →
x = 3 -1 = 1
Por lo tanto, la solución del sistema de ecuaciones es:
x = 1, y = 2
MATRICES
SUMA DE MATRICES : Para sumar dos matrices A y B deben ser de las mismas dimensiones, si esto es cierto, la suma es una matriz de iguales dimensiones que A y B, y sus elementos se obtienen sumando los elementos correspondientes de A y B.
PRODUCTO DE MATRICES POR UN ESCALAR
Así como se ha definido la suma de matrices, también se puede formar el producto de un numero real A y una matriz A. El resultado, denotado por A A, es la matriz cuyos elementos son los componentes de A multiplicados por A.

MULTIPLICACION DE MATRICES
Dos o mas matrices A y B son conformes en ese orden (primero A y despues B), si A tiene el mismo numero de columnas que B tiene de filas.

Así como se ha definido la suma de matrices, también se puede formar el producto de un numero real A y una matriz A. El resultado, denotado por A A, es la matriz cuyos elementos son los componentes de A multiplicados por A.

MULTIPLICACION DE MATRICES
Dos o mas matrices A y B son conformes en ese orden (primero A y despues B), si A tiene el mismo numero de columnas que B tiene de filas.

VECTORES
Las matrices donde M > 1 y N = 1, (es decir, están formadas por una sola columna) son llamadas matrices columnas o vectores. DE igual manera, si M = 1 y N > 1, se tiene una matriz fila o vector. Los vectores se denotaran con las letras minúsculas en negritas. Los vectores se denotaran con las letras minúsculas en negritas : B, X, etc. En estos casos no sera necesario la utilización de doble subindice para la identificación de sus elementos y un vector x de m elementos (en columna) queda simplemente como:
SUMA DE VECTORES
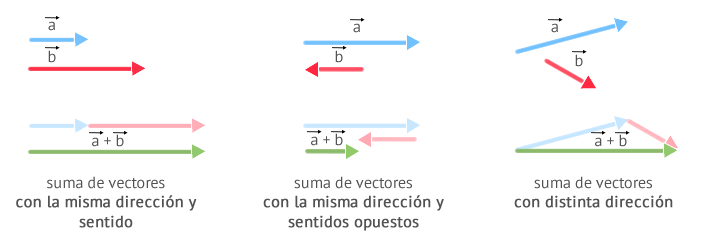
RESTA DE VECTORES

MULTIPLICACIÓN DE VECTORES

MÉTODO DE GAUSS
El método de Gauss para resolver un sistema de ecuaciones lineales consiste en obtener de un sistema:
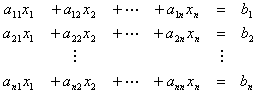
s. un sistema equivalente y escalonado, mediante transformaciones adecuadas.
Se pueden dar los siguientes pasos:
I. Si es necesario reordenar ecuaciones para que a11 sea distinto de cero.
II. Dividir la primera ecuación por a11 y restar a cada ecuación un múltiplo de la primera para eliminar todos los elementos que quedan por debajo de a11 x1 .
III. Repetir los pasos anteriores basados ahora en a22 (y si es necesario en cada aii).
IV. El proceso termina cuando no quedan más ecuaciones.
REGLA DE CRAMMER
Esta regla establece que cada incognita de un sistema de ecuaciones lineales algebraicas puede expresarse como una fracccion de dos determinantes con denominador d y con el numerador obtenido a partir de d, al reempazar a columna de coeficientes de la incognita en cuestion por contantes b1, b2 , ... , bn.
BIBLIOGRAFIA
https://www.portaleducativo.net/segundo-medio/45/sistema-de-ecuaciones-lineales
apuntes de la clase
Las matrices donde M > 1 y N = 1, (es decir, están formadas por una sola columna) son llamadas matrices columnas o vectores. DE igual manera, si M = 1 y N > 1, se tiene una matriz fila o vector. Los vectores se denotaran con las letras minúsculas en negritas. Los vectores se denotaran con las letras minúsculas en negritas : B, X, etc. En estos casos no sera necesario la utilización de doble subindice para la identificación de sus elementos y un vector x de m elementos (en columna) queda simplemente como:
SUMA DE VECTORES

RESTA DE VECTORES

MULTIPLICACIÓN DE VECTORES

MÉTODO DE GAUSS
El método de Gauss para resolver un sistema de ecuaciones lineales consiste en obtener de un sistema:
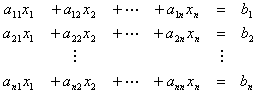
s. un sistema equivalente y escalonado, mediante transformaciones adecuadas.
Se pueden dar los siguientes pasos:
I. Si es necesario reordenar ecuaciones para que a11 sea distinto de cero.
II. Dividir la primera ecuación por a11 y restar a cada ecuación un múltiplo de la primera para eliminar todos los elementos que quedan por debajo de a11 x1 .
III. Repetir los pasos anteriores basados ahora en a22 (y si es necesario en cada aii).
IV. El proceso termina cuando no quedan más ecuaciones.
REGLA DE CRAMMER
Esta regla establece que cada incognita de un sistema de ecuaciones lineales algebraicas puede expresarse como una fracccion de dos determinantes con denominador d y con el numerador obtenido a partir de d, al reempazar a columna de coeficientes de la incognita en cuestion por contantes b1, b2 , ... , bn.
BIBLIOGRAFIA
https://www.portaleducativo.net/segundo-medio/45/sistema-de-ecuaciones-lineales
apuntes de la clase
No hay comentarios.:
Publicar un comentario